[자료구조] 트리(Tree) 구조
개념
- 자료구조 Tree는 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아서 트리 구조라고 부른다.
- 자료구조 Tree는 그래프의 여러 구조 중 무방향 그래프의 한 구조이다.
- 트리 구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조이다.
- 트리 구조는 데이터를 순차적으로 나열시킨 선형 구조가 아니라,
하나의 데이터 뒤에 여러 개의 데이터가 존재할 수 있는 비선형 구조이다. - 트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클이 없다.
- 트리 구조는 루트라는 하나의 꼭짓점 데이터를 시작으로, 여러 개의 데이터를 간선으로 연결한다.
- 트리 구조는 각 데이터를 노드라고 하며, 두 개의 노드가 상하계층으로 연결되면 부모/자식 관계를 가진다.
- 트리 구조에서 자식이 없는 노드는 나무의 잎과 같다고 하여 리프 노드라고 부른다.
- 자료구조 Tree는 깊이와 높이, 레벨 등을 측정할 수 있다.
Ex) 컴퓨터의 폴더 (Directory), 대진표, 가계도, 조직도 등
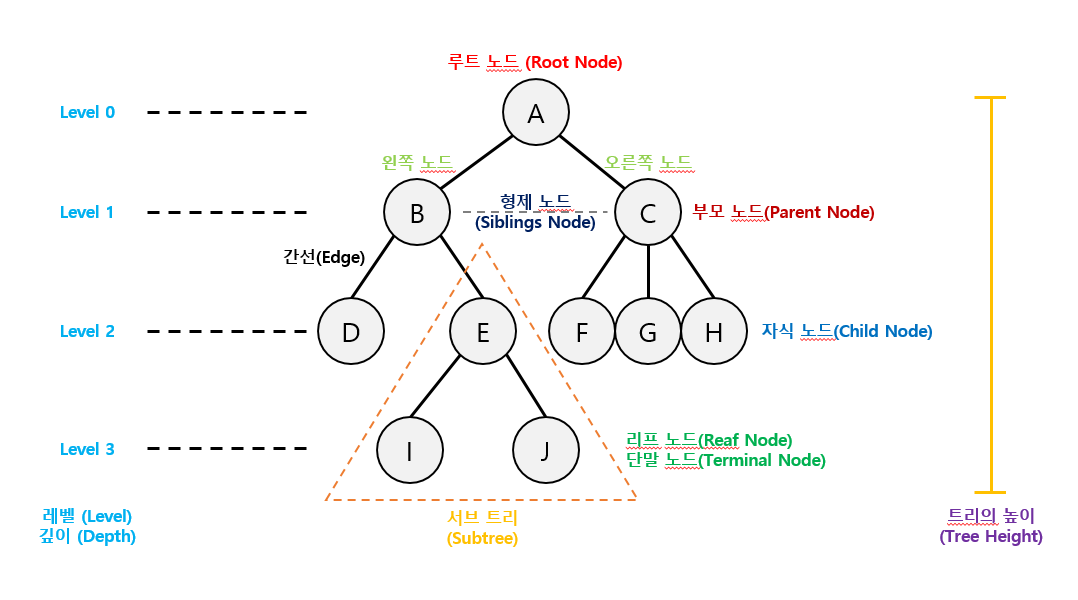
1. 트리는 하나의 루트 노드를 갖는다.
2. 루트 노드는 0개 이상의 자식 노드를 갖는다.
3. 자식 노드 또한 0개 이상의 자식 노드를 갖는다.
4. 노드(Node)들과 노드들을 연결하는 간선(Edge)들로 구성되어 있다.
트리의 구성요소
노드 (Node)
- 트리를 구성하고 있는 기본 요소
- 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있음.
- A, B, C, D, E, F, G, H, I, J
간선 (Edge)
- 노드와 노드 간의 연결선
루트 노드 (Root Node)
- 트리 구조에서 부모가 없는 최상위 노드
- root node : A
부모 노드 (Parent Node)
- 자식 노드를 가진 노드
- D, E에 부모 노드는 B
자식 노드 (Child node)
- 부모 노드의 하위 노드
- 노드 B의 자식 노드는 D, E
형제 노드 (Sibling node)
- 같은 부모를 가지는 노드
- B, C는 같은 부모(A)를 가지는 형제 노드
단말 노드 (terminal node), 리프 노드(leaf node), 외부 노드(external node, outer node)
- 자식 노드가 없는 노드
- D, F, G, H, I, J
깊이 (depth)
- 루트에서 어떤 노드까지의 간선(Edge) 수
- 루트 노드의 깊이 : 0
- D의 깊이 : 2
높이 (height)
- 루트 노드로부터 가장 멀리 있는 노드
- 이 트리의 높이는 I, J가 있는 Level 3
내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node)
- 자식 노드 하나 이상 가진 노드
서브트리
- 서브 트리란 트리 구조에서 root에서 뻗어나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 말한다.
- 그림에서 (D, H, I)로 이루어진 작은 트리도 서브 트리이고, (B, D, E)나 (C, F, G, H)도 서브 트리이다.
트리 순회 (Tree Traversal)
트리의 모든 노드들을 방문하는 과정을 트리 순회(TreeTraversal)라고 한다.
선형 자료 구조(연결 리스트, 스택, 큐 등)는 순차적으로 요소에 접근하지만 트리 자료구조는 다른 방식을 사용해야 한다.
일반적으로 트리 순회에는 다음과 같은 방법들이 있다.
- 전위 순회 (Preorder)
- 중위 순회 (Inorder)
- 후위 순회 (Postorder)
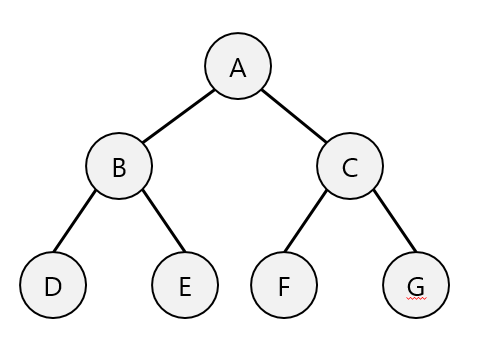
전위 순회 (Preorder Traversal)
- 깊이 우선 순회(DFT, Depth-First Traversal)라고도 한다.
- 전위 표기법(연산자를 먼저 표시하고 연산에 필요한 피연산자를 나중에 표기하는 방법)을 구하는데 사용
- 전위 순회 방법
- Root 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
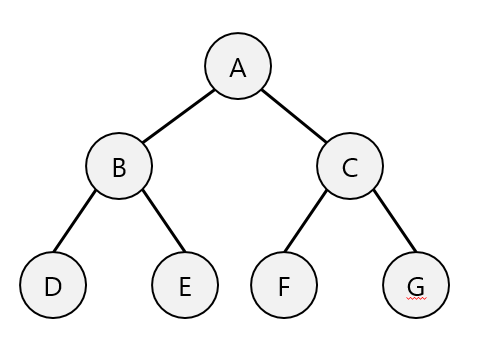
중위 순회 (Inorder Traversal)
- 중위 순회는 대칭 순회(symmetric traversal)라고도 한다.
- 중위 표기법(연산자를 두 피연산자 사이에 표기하는 방법으로 가장 일반적으로 사용되는 표현 방법)을 구하는데 사용
- 이진 탐색트리(BST)에서 오름차순 또는 내림차순으로 값을 가져올 때 사용
- 내림차순으로 값을 가져오기 위해서는 역순(오른쪽-> root-> 왼쪽)으로 중위 순회를 한다.
- 중위 순회 방법
- 왼쪽 서브 트리를 중위 순회한다.
- Root 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
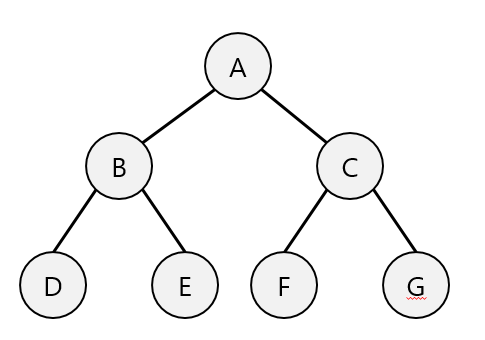
후위 순회 (Postorder Traversal)
- 후위 표기법(피연산자를 먼저 표시하고 연산자를 나중에 표시하는 방법)을 구하는데 사용
- 스택을 사용하는 예들 중 가장 빈번하게 등장한다.
- 트리를 삭제하는데 주로 사용
- 후위 순회 방법
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- Root 노드를 방문한다.
트리의 종류
이진 트리(Binary Tree)
- 최대 2개의 자식노드를 가진 트리
힙 (Heap)
- 부모 자식간 대소 관계는 정의되어 있으나 형제간의 대소 관계는 정의되어 있지 않은 완전 이진트리 구조
- 최대 힙, 최소 힙 두 종류가 있다.
포화 이진 트리(Perfect Binary Tree)
- 모든 리프 노드가 똑같은 레벨에 있는 경우의 트리
- 마지막 레벨의 노드가 가득 차 있는 경우
정 이진 트리(Full Binary Tree)
- 모든 노드가 0 or 2개의 자식노드를 가지고 있는 트리
편향 이진 트리(Skewed Binary Tree)
- 모든 노드들이 한 방향으로 편향된 트리
그 외 검색 트리의 분류
- 일차원 검색 트리(키를 구성하는 필드가 하나)
- 이진 검색 트리
- 다진 검색 트리
- B-트리
- AVL-트리
- 레드 블랙 트리
- 다차원 검색 트리(키를 구성하는 필드가 두개 이상)
- KD-트리
- KDB-트리
- R-트리
'Thinking > data structure' 카테고리의 다른 글
| B-트리 (B-Tree) (0) | 2023.10.03 |
|---|---|
| 레드 블랙 트리 (Red-Black Tree) (0) | 2023.10.02 |
| 이진 탐색 트리 (BST : Binary Search Tree) (0) | 2023.10.02 |
| 메모리 구조 (코드영역, 데이터영역, 힙영역, 스택영역) (0) | 2022.12.20 |
| 1Byte는 왜 8bit일까? (0) | 2022.09.28 |


