반응형
선택 (Select) 알고리즘
정렬되지 않은 리스트나 배열에서 가장 작은 k번째 수를 찾는 알고리즘이다.
간단한 방법은 최소 숫자들을 오름차순으로 정렬한 후, k번째 숫자를 찾는 것이 있는데, 이러한 알고리즘은 O(nlogn)의 수행 시간이 걸린다. 이보다 효율적인 해결을 위하여 분할 정복 개념을 활용할 수 있다.
- 일부 과정이 퀵 정렬과 비슷하여 Quick-Select 알고리즘이라고도 한다.
- "평균"선형 시간 안에 k번째 작은 수를 찾을 수 있다.
- 부분문제의 크기가 일정하지 않은 크기가 감소하는 형태의 분할 정복 알고리즘이다.
- 만일 피봇이 입력을 너무 한 쪽으로 치우치게 분할하면, 알고리즘의 수행시간이 길어진다.
- 두 그룹 중 하나의 크기가 입력 크기의 3/4과 같거나 그보다 크면 bad 분할이고, 그 반대의 경우는 good 분할이다.
과정
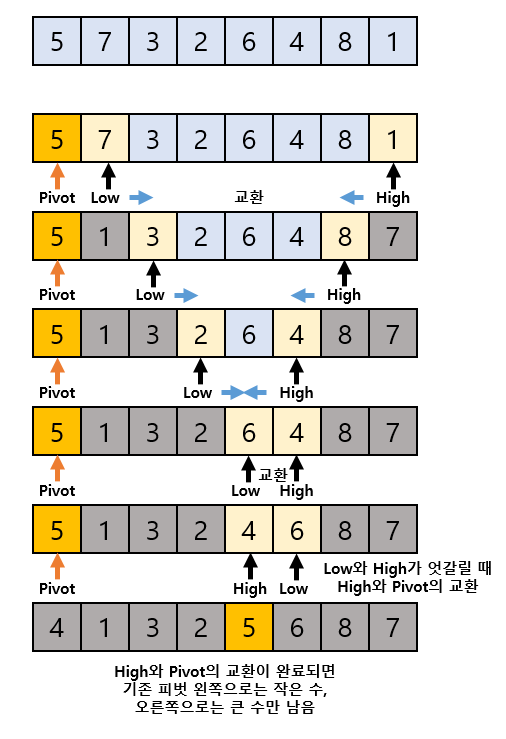
- 선택 문제는 입력이 정렬되어 있지 않으므로, 퀵 정렬과 마찬가지로 피봇을 선택하여 피봇보다 작은 숫자들은 피봇의 왼쪽으로, 큰 숫자들은 피봇의 오른쪽 숫자로 이동시킨다.
- 이렇게 2개로 분할된 그룹들의 크기를 각각 파악하면, k번째로 작은 숫자가 2개의 그룹 중 어디에 속해있는 지를 알 수 있다.
- 원하는 숫자가 속해 있지 않은 그룹은 고려하지 않고, 숫자가 속해 있는 그룹에서 위와 같은 작업을 반복하여 k번째로 작은 숫자를 파악한다.
퀵 정렬 알고리즘 참고하기
반응형
'Thinking > Algorithm' 카테고리의 다른 글
| Sort 계수 정렬 (Counting Sort) 알고리즘 (0) | 2023.10.01 |
|---|---|
| Sort 기수 정렬 (Radix Sort) 알고리즘 (0) | 2023.10.01 |
| Sort 힙 정렬(Heap Sort) 알고리즘 (0) | 2023.09.19 |
| Sort 퀵 정렬(Quick Sort) 알고리즘 (0) | 2023.09.14 |
| Sort 병합 정렬(Merge Sort) 알고리즘 (0) | 2023.09.13 |



