반응형
[Sort] 힙 정렬(Heap Sort) 알고리즘
힙(Heap)이란?
힙이란 완전 이진 트리의 형태로 만들어진 자료구조이다.
돌 더미, 장작 더미 처럼 위로 갈수록 노드의 수가 줄어드는 모습을 하고 있다.
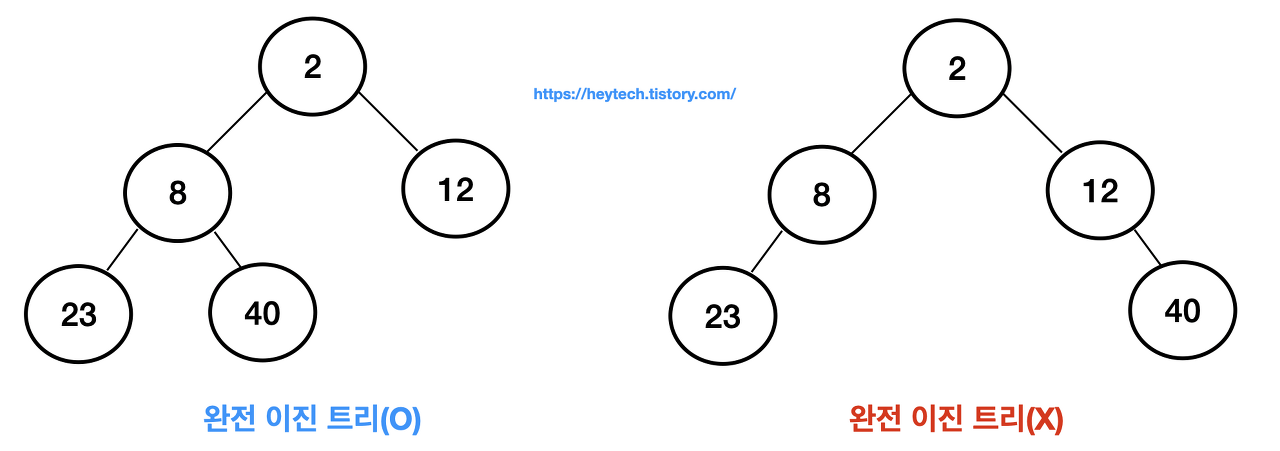
완전 이진 트리(Complete Binary Tree)란?
완전 이진 트리란 각 노드가 최대 2개의 자식 노드를 가지고 마지막 레벨을 제외한 모든 노드는 완전히 채워져 있는 자료구조이다. 최하단 레벨의 노드는 좌측 노드가 채워져 있거나 좌측과 우측 모두 채워져 있어야 하며, 노드를 삽입할 때는 최하단 좌측 노드부터 차례대로 삽입해야 한다.
힙 정렬(Heap Sort)이란 ?
- 힙 정렬(Heap sort)이란 최대 힙(부모 노드 > 자식 노드) 트리나 최소 힙(부모 노드 < 자식 노드) 트리를 구성해 정렬을 하는 방법이다.
- 힙(heap)이라는자료구조는 J.W.J. 윌리엄스(Williams)라는 영국의 컴퓨터과학자가 1964년에 힙 정렬 알고리즘을 고안하면서 최초로 설계 되었다.
- 대표적으로 우선순위 큐뿐 아니라 이를 이용한 다익스트라 알고리즘에도 활용된다.
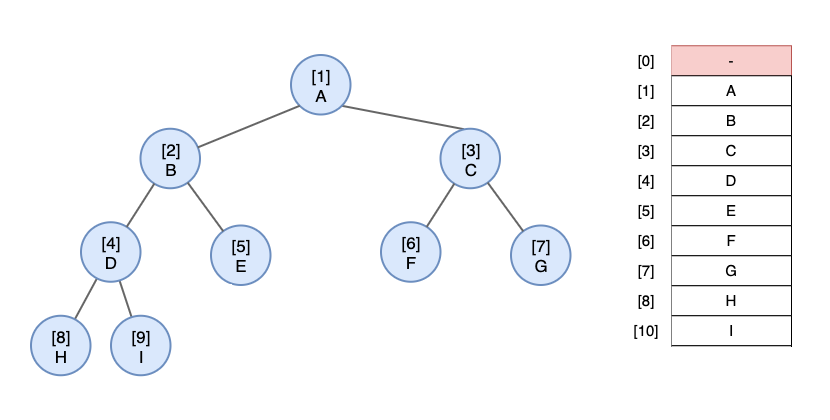
힙(Heap)의 표현 방법
힙 구조 구현
/*
* 부모는 a[(i - 1) / 2]
* 왼쪽 자식은 a[(i * 2) + 1]
* 오른쪽 자식은 a[(i * 2) + 2]
*/
#include <iostream>
using namespace std;
#define MAX_HEAP_SIZE 100
void HeapifyUp(int arr[], int n);
void HeapifyDown(int arr[], int n, int heapCount);
void HeapSort(int arr[], int n);
void InsertHeap(int arr[], int value, int heapCount);
void DeleteHeap(int arr[], int heapCount);
void Swap(int& a, int& b);
void PrintHeap(int arr[], int count);
int main()
{
int heap[MAX_HEAP_SIZE];
int heapCount = 0;
int insertData[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int length = sizeof(insertData) / sizeof(insertData[0]);
for (int i = 0; i < length; i++)
{
InsertHeap(heap, insertData[i], heapCount);
heapCount++;
}
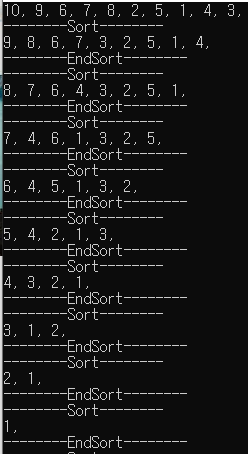
PrintHeap(heap, heapCount);
for (int i = 0; i < length; i++)
{
cout << "--------Sort--------" << endl;
DeleteHeap(heap, heapCount);
heapCount--;
PrintHeap(heap, heapCount);
cout << "--------EndSort--------" << endl;
}
//PrintHeap(heap, heapCount);
}
void HeapifyUp(int arr[], int n)
{
if (n == 0)
return;
int parent = (n - 1) / 2;
if (arr[parent] < arr[n])
{
Swap(arr[parent], arr[n]);
HeapifyUp(arr, parent);
}
}
void HeapifyDown(int arr[], int n, int heapCount)
{
int leftChild = n * 2 + 1;
int rightChild = n * 2 + 2;
int target = leftChild;
if (leftChild >= heapCount)
return;
if (rightChild < heapCount)
{
if (arr[leftChild] < arr[rightChild])
{
target = rightChild;
}
}
Swap(arr[target], arr[n]);
HeapifyDown(arr, target, heapCount);
}
void InsertHeap(int arr[], int value, int heapCount)
{
if (heapCount >= MAX_HEAP_SIZE)
return;
arr[heapCount] = value;
HeapifyUp(arr, heapCount);
heapCount++;
}
void DeleteHeap(int arr[], int heapCount)
{
Swap(arr[0], arr[heapCount]);
arr[heapCount] = 0; // 삭제
HeapifyDown(arr, 0, heapCount);
}
void Swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
void PrintHeap(int arr[], int count)
{
for (int i = 0; i < count; i++)
{
cout << arr[i] << ", ";
}
cout << "\n";
}
반응형
'Thinking > Algorithm' 카테고리의 다른 글
| Sort 계수 정렬 (Counting Sort) 알고리즘 (0) | 2023.10.01 |
|---|---|
| Sort 기수 정렬 (Radix Sort) 알고리즘 (0) | 2023.10.01 |
| Sort 퀵 정렬(Quick Sort) 알고리즘 (0) | 2023.09.14 |
| Sort 병합 정렬(Merge Sort) 알고리즘 (0) | 2023.09.13 |
| Sort 삽입 정렬(Insertion Sort) 알고리즘 (0) | 2023.09.03 |



