KD-트리 (K-Dimensional Tree) [k-차원 트리]
KD-트리는 이진 탐색 트리를 확장한 것으로 k개(k>=2)의 필드로 이루어지는 키를 사용한다.
- 동일한 레벨에 있는 노드는 모두 동일한 하나의 필드만 이용해서 분기한다


KD-트리에서 검색을 이용해 내려간다는 것은 다차원 공간에서 이렇게 나누어진 결과에 따라 공간의 범위를 점점 좁혀나가는 것이다. 3차원일 경우 입체적인 형상이 된다.
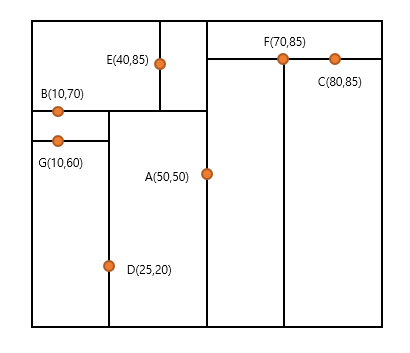
KD-트리 삽입

A(50, 50) → B(10, 70) → C(80, 85) → D(25, 20) → E(40, 85) → F(70, 85) → G(10, 60)
1. A(50, 50)이 루트 자리를 차지
2. B(10, 70)는 x값 10이 루트의 x값 50보다 작으므로 왼쪽 자식이 된다
3. C(80, 85)는 x값 80이 루트의 x값 50보다 크므로 오른쪽 자식이 된다
4. D(25, 20)는 먼저 x값 25가 루트의 x값 50보다 작으므로 루트의 왼쪽으로 가서 B(10, 70)를 만난다
y값 20이 B의 y값 70보다 작으므로 B의 왼쪽 자식이 된다
5. E(40, 85)는 x값 40의 루트의 x값 50보다 작고, y보다 85가 B의 y값 70보다 크므로 B의 오른쪽 자식이 된다
6. F(70, 85)는 x값 70이 루트의 x값 50보다 크고, y값 85가 C의 y값 85와 같으므로 B의 오른쪽 자식이 되었다.
7. G(10, 60)는 x값 10이 루트의 x값 50보다 작고, y값 60이 B의 y값 70보다 작고,
x값 10이 D의 x값 25보다 작으므로 D의 왼쪽 자식이 된다.
KD-트리 삭제
- 자식이 없는 경우 : 이진 검색 트리와 마찬가지로 노드 r만 제거하면 된다.
- 자식이 둘인 경우 :
- 오른쪽 서브 트리 중 노드 r에서 분기에 사용한 필드값이 가장 작은 노드를 찾아 삭제하고 그 노드를 노드 r의 자리로 이동한다.
- 자식이 하나뿐인 경우에도 높은 확률로 KD-트리의 성질이 깨지므로 r의 부모가 r의 자식을 가리키도록 하는 것은 안된다.
- 왼쪽 자식 하나만 있을 경우 왼쪽 서브 트리 중 노드 r에서 분기에 사용한 필드 값이 가장 큰 노드를 찾아 삭제하고 노드 r의 자리로 이동한다.
'Thinking > data structure' 카테고리의 다른 글
| B-트리 (B-Tree) (0) | 2023.10.03 |
|---|---|
| 레드 블랙 트리 (Red-Black Tree) (0) | 2023.10.02 |
| 이진 탐색 트리 (BST : Binary Search Tree) (0) | 2023.10.02 |
| 자료구조 트리(Tree) 구조 (0) | 2023.09.22 |
| 메모리 구조 (코드영역, 데이터영역, 힙영역, 스택영역) (0) | 2022.12.20 |



