반응형
[Sort] 병합 정렬(Merge Sort) 알고리즘
병합정렬이란?
병합 정렬(Merge Sort)은 분할 정복(Divide and Conquer) 방식을 이용한다. 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다. 병합하는 과정에서 재귀적으로 반복하며 풀어내는 것이 일반적이다.
- '존 폰 노이만(John von Neumann)'이 1945년에 개발
- 데이터 분포도에 영향을 많이 받지 않아 시간복잡도가 O(NlogN)인 안정적인 정렬 방식에 속한다.
- 두 개의 배열을 병합할 때 병합 결과를 담아 놓을 배열이 추가로 필요하다. 따라서 공간 복잡도는 O(N) 이다.
- 다른 정렬 방법은 연결리스트에서 각 데이터에 접근을 필요로 하지만 병합정렬은 직접 접근을 할 필요가 없다. 따라서 연결 리스트를 정렬하는데 적합한 알고리즘이다. (연결리스트는 순차 접근)
- 분할 정복 (Divide and Conquer) 방식을 이용한다.
- 분할(Divide) : 리스트를 두 개의 리스트로 분할한다.
- 정복(Conquer) : 분할된 리스트를 정렬한다. 분할된 리스트가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine): 정렬된 두 개의 리스트를 하나의 정렬된 리스트로 결합한다.
병합정렬 예시
- 1~8까지 숫자가 중복 없이 무작위 위치에 저장되어 있다고 가정한다.
- 자료는 오름차순으로 정렬한다.
- 병합정렬은 재귀적으로 풀어낸다.
- 리스트를 더 이상 나눌 수 없을 때 까지 분할한다.
- 분할된 리스트를 다시 결합한다. 결합은 반으로 분할된 리스트를 서로 비교 정렬하면서 결합한다.
- 결합된 리스트들은 정렬이 되어 있는 상태이다.
- 정렬이 되어 있기 때문에 왼쪽 리스트와 오른쪽 리스트의 가장 앞 부분만 비교한다.
- 왼쪽 리스트와 오른쪽 리스트의 비교 기준(비교 대상 자료를 가리킴)이 되는 인덱스가 필요하다.
- 한쪽 리스트가 먼저 비어있을 경우 나머지를 순서대로 옮긴다.

결합되는 과정은 다음과 같다.
- 왼쪽 리스트와 오른쪽 리스트의 가장 작은(가장 앞에있는) 자료를 비교한다.
- 더 작은 자료를 정렬된 리스트에 삽입한다.
- 작은 자료가 빠진 리스트의 인덱스를 하나 증가시킨다.
- 한 쪽 리스트가 비어있을 때 까지 반복한다.
- 아직 자료가 남은 리스트는 순서대로 정렬된 리스트로 옮긴다.
- 이 결합 과정을 최종 정렬까지 반복한다.

#include <iostream>
#define MAX_SIZE 8
using namespace std;
void merge_sort(int list[], int left, int right);
void merge(int list[], int left, int mid, int right);
int sorted[MAX_SIZE];
int main()
{
int originData[MAX_SIZE] = { 5, 7, 3, 2, 6, 4, 8, 1 };
merge_sort(originData, 0, MAX_SIZE-1);
// 데이터 확인
cout << endl;
for (int i = 0; i < MAX_SIZE; i++) {
cout << originData[i] << " ";
}
return 0;
}
void merge_sort(int list[], int left, int right) {
int mid;
if (left < right) {
mid = (left + right) / 2; // 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
merge_sort(list, left, mid); // 앞쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, mid + 1, right); // 뒤쪽 부분 리스트 정렬 -정복(Conquer)
merge(list, left, mid, right); // 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
}
}
void merge(int list[], int left, int mid, int right)
{
int i, j, k, l;
i = left;
j = mid + 1;
k = left;
/* 분할 정렬된 list의 합병 */
while (i <= mid && j <= right) {
if (list[i] <= list[j])
sorted[k++] = list[i++];
else
sorted[k++] = list[j++];
}
// 남아 있는 값들을 일괄 복사
if (i > mid) {
for (l = j; l <= right; l++)
sorted[k++] = list[l];
}
// 남아 있는 값들을 일괄 복사
else {
for (l = i; l <= mid; l++)
sorted[k++] = list[l];
}
// 배열 sorted[](임시 배열)의 리스트를 배열 list[]로 재복사
for (l = left; l <= right; l++) {
list[l] = sorted[l];
}
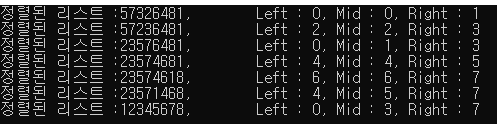
cout << "정렬된 리스트 :";
for (int i = 0; i < sizeof(list); i++)
{
cout << list[i];
}
cout << ",\tLeft : " << left << ", Mid : " << mid << ", Right : " << right << endl;
}
반응형
'Thinking > Algorithm' 카테고리의 다른 글
| Sort 힙 정렬(Heap Sort) 알고리즘 (0) | 2023.09.19 |
|---|---|
| Sort 퀵 정렬(Quick Sort) 알고리즘 (0) | 2023.09.14 |
| Sort 삽입 정렬(Insertion Sort) 알고리즘 (0) | 2023.09.03 |
| Sort 버블 정렬(Bubble Sort) 알고리즘 (0) | 2023.09.03 |
| Sort 선택 정렬(Selection Sort) 알고리즘 (0) | 2023.09.02 |



